Quiz powtórzeniowy Praca, moc, energia mechaniczna

Zaznacz zdanie, które poprawnie opisuje iloczyn skalarny
wektorów \(\overrightarrow{a}\) i \(\overrightarrow{b}\).
Iloczyn skalarny jest zawsze liczbą nieujemną.
Iloczyn skalarny jest przemienny.
Iloczyn skalarny jest zdefiniowany wzorem \(\overrightarrow{a}\)∙\(\overrightarrow{b}\)=|\(\overrightarrow{a}\)|∙|\(\overrightarrow{b}\)|∙\(\,\text{sin}\,α\), gdzie \(α\,\)jest kątem między wektorami.
Iloczyn skalarny niezerowych wektorów jest równy zeru, gdy wektory są do siebie równoległe.
Na poruszające się ciało o masie \(20\,\text{kg}\) działała siła tarcia kinetycznego o wartości \(80\,\text{N}\) i spowodowała zatrzymanie ciała na drodze \(2\,\text{m}\).
Zaznacz odpowiedź na pytanie.
Jaką pracę wykonała ta siła?
- \(-160\,\text{J}\)
- \(160\,\text{J}\)
- \(40\,\text{J}\)
- \(-40\,\text{J}\)
Ciało o masie \(2\,\text{kg}\) osiągnęło prędkość \(4\,\frac{\text{m}}{\text{s}}\) w czasie \(8\) sekund.
Zaznacz odpowiedź na pytanie.
Jaka była średnia moc tego ciała?
- \(1\,\text{W}\)
- \(2{,}5\,\text{W}\)
- \(0{,}5\,\text{W}\)
- \(2\,\text{W}\)
Wykres przedstawia zależność mocy chwilowej od czasu dla pewnego urządzenia.
Zaznacz odpowiedź na pytanie.
Ile wynosiła praca wykonana w czasie \(10\) sekund przez to urządzenie i jego średnia moc?
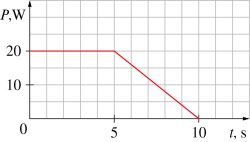
\(50\,\text{J}\); \(5\,\text{W}\)
\(100\,\text{J}\); \(10\,\text{W}\)
\(150\,\text{J}\); \(15\,\text{W}\)
\(200\,\text{J}\); \(20\,\text{W}\)
Samolot lecący na wysokości \(2000\) stóp wzniósł się na wysokość \(4000\) stóp, zwiększając jednocześnie prędkość z \(200\) węzłów do \(400\) węzłów.
Zaznacz odpowiedź na pytanie.
Jak zmieniły się energia potencjalna grawitacji i kinetyczna samolotu?
Energia potencjalna wzrosła 2 razy i kinetyczna wzrosła 4 razy.
Energia potencjalna wzrosła 2 razy, a kinetyczna wzrosła 2 razy.
Energia potencjalna wzrosła 4 razy, a kinetyczna wzrosła 4 razy.
Nie można odpowiedzieć na to pytanie, dopóki nie wyrazi się stóp i węzłów w jednostkach układu SI.
Ciało spada z wysokiej wieży (bez prędkości początkowej). Jego prędkość w połowie wysokości wieży wynosi \(20\,\frac{\text{m}}{\text{s}}\). Pomiń opory ruchu i przyjmij, że ziemskie pole grawitacyjne jest jednorodne.
Zaznacz zdanie poprawnie opisujące ten ruch.
Wartość siły ciężkości rośnie w czasie spadania.
Ciało uderzy w ziemię z prędkością \(40\,\frac{\text{m}}{\text{s}}\).
Energia kinetyczna tego ciała w połowie wysokości wieży równa jest połowie jego początkowej energii potencjalnej.
Wieża miała wysokość \(20\,\text{m}\).
Trzy ciała zaczynają zsuwać się jednocześnie bez tarcia z wysokości \(h\) po torach przedstawionych na rysunku.
Zaznacz odpowiedź na pytanie.
Które z nich osiągnie w punkcie \(P\) największą prędkość?
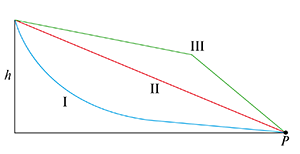
I
II
III
Wszystkie ciała osiągną taką samą prędkość.
Trzy ciała zaczynają zsuwać się jednocześnie bez tarcia z wysokości \(h\) po torach przedstawionych na rysunku.
Zaznacz odpowiedź na pytanie.
Które z ciał jako pierwsze dotrze do punktu \(P\) ?

I
II
III
Wszystkie ciała dotrą jednocześnie.
Zaznacz zdanie prawdziwe.
W zderzeniach niesprężystych jest zachowana energia kinetyczna.
Zderzenie i połączenie dwóch plastelinowych kul jest przykładem zderzenia sprężystego.
W zderzeniach niesprężystych nie jest zachowany pęd.
Energię kinetyczną ciała i wartość jego pędu łączy wzór \(E_\text{k}=\frac{p^2}{2m}\).
Rysunek przedstawia położenia, masy i prędkości dwóch kul chwilę przed sprężystym
i centralnym ich zderzeniem.
Zaznacz zdanie poprawnie opisujące tę sytuację.
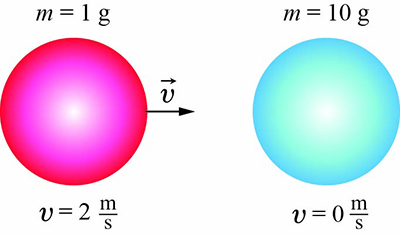
Prędkość kuli o masie \(1\,\text{g}\) będzie po zderzeniu zwrócona w prawo.
Podczas zderzenia kule się połączą.
Całkowita energia kinetyczna kul po zderzeniu będzie mniejsza niż energia kinetyczna przed zderzeniem.
Prędkość kuli o masie \(1\,\text{g}\) będzie miała po zderzeniu wartość mniejszą niż \(2\frac{\text{m}}{\text{s}}\).
Zaznacz zdanie nieprawdziwe.
Jeśli do urządzenia dostarczono \(100\,\text{J}\) energii, z której \(30\,\text{J}\) zostało stracone (rozproszone), to sprawność urządzenia \(η=0{,}7\).
Dzięki zastosowaniu maszyn prostych możliwe jest zmniejszenie wartości siły niezbędnej do wykonania pracy.
Dzięki zastosowaniu maszyn prostych możliwe jest uzyskanie sprawności większej niż \(1\).
Sprawność jest wielkością bezwymiarową (jak współczynnik tarcia lub sinus kąta).
Zaznacz odpowiedź na pytanie.
Czy ciało o masie \(100\,\text{kg}\) może być wciągnięte po równi pochyłej za pomocą siły o wartości \(10\,\text{N}\)? Pomiń tarcie.
Tak, o ile kąt nachylenia równi jest odpowiednio mały.
Tak, o ile kąt nachylenia równi jest odpowiednio duży.
Nie, ponieważ ciężar tego ciała jest wielokrotnie większy niż \(10\,\text{N}\).
Nie, ponieważ do wciągnięcia ciała o masie \(100\,\text{kg}\) niezbędna jest siła \(100\,\text{N}\).

Chcesz wiedzieć więcej?
Podając adres e-mail, wyrażasz zgodę na otrzymywanie od WSiP informacji handlowych dotyczących produktów i usług WSiP przekazywanych za pomocą telekomunikacyjnych urządzeń końcowych oraz tzw. automatycznych systemów wywołujących, drogą elektroniczną na podany adres e-mail.